Tembereng Adalah – Tembereng lingkaran adalah salah satu konsep dasar dalam geometri yang sering kali dibahas dalam dunia pendidikan. Namun, tak jarang konsep ini dapat membingungkan bagi banyak orang. Tembereng lingkaran tidak hanya penting untuk pemahaman teoretis, tetapi juga memiliki berbagai aplikasi praktis dalam kehidupan sehari-hari.

Artikel ini akan membahas secara lengkap mengenai gambar tembereng lingkaran, mulai dari pengertiannya, rumus perhitungannya, hingga aplikasinya dalam berbagai bidang.

Daftar Isi tampilkan

Tembereng Lingkaran Adalah ?

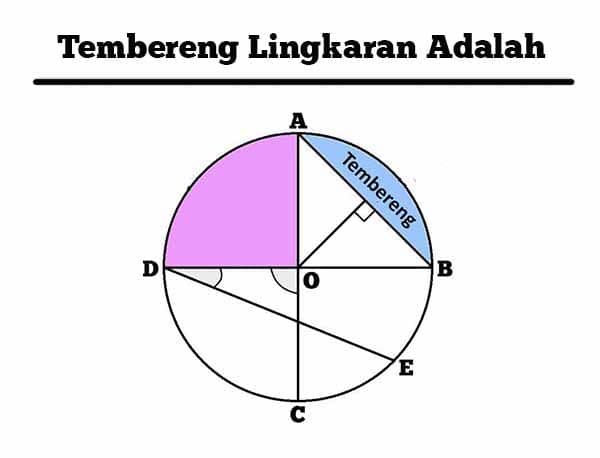
Apa itu tembereng lingkaran ? Tembereng lingkaran adalah luas daerah pada lingkaran yang terbentuk dan dibatasi oleh tali busur dan busur lingkaran.

Tembereng dibatasi oleh sebuah tali busur dan juga busur lingkaran. Posisi tembereng juga berada di dalam juring lingkaran.

Bagian lingkaran lain yang menyusun sebuah bangun lingkaran yaitu jari jari lingkaran, diameter lingkaran, apotema lingkaran, juring lingkaran, busur lingkaran, sudut pusat lingkaran dan sudut keliling lingkaran.

Bentuk tembereng lingkaran akan diberikan pada bagian gambar tembereng lingkaran.

Unsur-Unsur Tembereng Lingkaran

Untuk memahami tembereng lingkaran, kita perlu mengenal unsur-unsur berikut:

Lingkaran : Setiap titik pada bidang yang berjarak sama dari satu titik pusat.
Busur : Bagian dari lingkaran yang diapit oleh dua titik pada lingkaran tersebut.
Tali Busur : Garis lurus yang menghubungkan dua titik pada lingkaran tanpa melalui pusat.
Juring Lingkaran : Daerah yang dibatasi oleh dua radius dan busur lingkaran.

Rumus Luas Tembereng

Cara mencari luas tembereng lingkaran adalah dengan menghitung menggunakan rumus. Rumusnya adalah dengan mencari tau luas juring kemudian dikurangi luas segitiga yang ada di dalam juring.

Rumus tembereng lingkaran yaitu sebagai berikut.

Rumus Luas Tembereng = Luas Juring Lingkaran – Luas Segitiga di Dalam Juring

atau

Keterangan :
a = besar sudut pusat lingkaran
r = jari jari lingkaran
t = tinggi segitiga
π = phi (22/7 atau 3,14)

Gambar Tembereng Lingkaran

Garis tembereng lingkaran sudah dijelaskan dengan lengkap diatas mulai dari pengertian hingga rumusnya. Untuk lebih memahami mengenai materi ini, akan diberikan contoh gambarnya.

Contoh tembereng lingkaran yaitu sebagai berikut.

Contoh Penggunaan Tembereng Lingkaran di Kehidupan Sehari-hari

Penggunaan konsep tembereng lingkaran melampaui klasifikasi matematika murni, aplikasi nyata ditemukan dalam desain arsitektur dan teknik. Beberapa contoh penerapannya antara lain:

Jembatan dan Bangunan : Banyak struktur melengkung, seperti jembatan dan bangunan berkubah, menggunakan prinsip tembereng untuk menjaga keseimbangan dan distribusi beban.
Desain Produk dan Seni : Dalam pembuatan desain simetris dan estetis, tembereng lingkaran sering digunakan untuk menciptakan pola yang harmonis.
Optik : Dalam desain lensa dan instrumen optik, perhitungan bagian melingkar dapat melibatkan penggunaan tembereng lingkaran.

Kesimpulan Tembereng Lingkaran

Tembereng lingkaran merupakan salah satu konsep dasar dalam geometri yang memiliki banyak aplikasi praktis. Memahami rumus dan penerapannya dapat membantu proses pembelajaran dan penggunaan dalam berbagai bidang. Dengan menguasai konsep ini, kita dapat lebih mudah memecahkan permasalahan geometris dan menjelajahi kreativitas dalam desain dan arsitektur.

Contoh gambar tembereng dan penjelasannya sudah diberikan dengan lengkap diatas. Semoga tulisan ini bisa bermanfaat bagi para pembaca. Jika terdapat kekurangan atau kesalahan dalam penulisan dan ingin memberikan kritik atau saran, bisa ditulis di kolom komentar.