7 Contoh Segi Banyak Tidak Beraturan : Ciri Ciri & Gambar

Segi Banyak Tidak Beraturan – Postingan ini menjelaskan tentang contoh segi banyak tidak beraturan disertai gambar dan juga penjelasannya.

Gambar segi banyak tidak beraturan dan pembahasannya yaitu sebagai berikut.

Daftar Isi tampilkan

Segi Banyak Tidak Beraturan Adalah

Segi banyak tidak beraturan adalah bentuk geometri yang memiliki beberapa sisi dan sudut, namun tidak memiliki bentuk yang teratur atau simetris.

Segi banyak tidak beraturan, juga dikenal sebagai poligon tidak beraturan, merujuk pada poligon yang tidak memiliki sisi-sisi dan sudut-sudut yang seragam atau terdefinisi dengan jelas.

Poligon tidak beraturan menampilkan variasi dalam panjang sisi-sisi dan ukuran sudut-sudutnya, menciptakan bentuk yang kompleks dan tidak teratur.

Dalam segi banyak tidak beraturan, sisi-sisinya memiliki panjang yang bervariasi. Tidak ada keseragaman panjang sisi seperti yang ditemukan dalam segi banyak beraturan.

Selain itu, sudut-sudut pada poligon tidak beraturan juga memiliki ukuran yang bervariasi. Tidak ada pola sudut yang konsisten seperti pada segi banyak beraturan.

Variasi dalam panjang sisi dan ukuran sudut pada poligon tidak beraturan menciptakan bentuk yang kompleks dan tidak teratur. Bentuk poligon dapat memiliki sisi-sisi yang memanjang atau memendek secara acak dan sudut-sudut yang tumpang tindih atau terpisah secara bebas.

Ciri Ciri Segi Banyak Tidak Beraturan

Terdapat perbedaan antara bangun segi banyak tidak beraturan dengan segi banyak beraturan. Untuk mengetahui perbedaan dari kedua bangun tersebut, kita perlu mengetahui ciri ciri segi banyak tidak beraturan.

Ciri-ciri segi banyak tidak beraturan yaitu sebagai berikut :

Memiliki sisi-sisi dengan panjang yang berbeda-beda. Tidak ada keseragaman panjang sisi seperti pada segi banyak beraturan. Sisi-sisi poligon tidak beraturan bisa memanjang atau memendek secara acak.
Memiliki sudut-sudut dengan ukuran yang bervariasi. Tidak ada pola sudut yang konsisten seperti pada segi banyak beraturan. Sudut-sudut pada poligon tidak beraturan dapat tumpang tindih atau terpisah secara bebas.
Poligon tidak beraturan menampilkan bentuk yang kompleks dan tidak teratur. Kekurangan struktur yang terdefinisi membuatnya menantang untuk dianalisis dan dipelajari. Bentuk poligon bisa memiliki sisi-sisi yang melengkung atau berlekuk-lekuk, serta sudut-sudut yang tidak teratur.
Karena variasi dalam panjang sisi dan ukuran sudut, segi banyak tidak beraturan memberikan variasi visual yang menarik. Bentuk poligon yang tidak teratur menciptakan tampilan yang unik dan tidak konvensional, menarik perhatian dan menantang persepsi.
Segi banyak tidak beraturan tidak mengikuti pola matematis yang konsisten. Keberadaan sisi-sisi dan sudut-sudut yang tidak beraturan mencerminkan ketidakteraturan dan kebebasan dalam bentuk poligon tersebut.

Contoh Segi Banyak Tidak Beraturan

Bangun segi banyak tidak beraturan yaitu segitiga sama kaki, segitiga sembarang, persegi panjang, trapesium, belah ketupat, jajar genjang dan layang layang.

Dari semua bangun tersebut, memiliki ciri ciri dan karakteristik yang berbeda antara bangun datar.

Gambar segi banyak tidak beraturan dan penjelasannya yaitu sebagai berikut.

• Segitiga Sama Kaki

Segi banyak tidak beraturan yang pertama adalah segitiga sama kaki. Segitiga sama kaki adalah bangun datar segitiga yang pada kedua sisinya selain sisi alas memiliki panjang yang sama.

Jika pada segitiga sama sisi, ketiga sisinya memiliki panjang yang sama. Sedangkan pada segitiga sama kaki hanya kedua sisinya yang sama panjang.

Sifat sifat segitiga sama kaki yaitu :
• Memiliki 3 sisi yang terdiri dari 2 sisi yang sama panjang
• Memiliki 3 sudut yang terdiri dari 2 sudut yang sama besar
• Memiliki 1 simetri putar
• Memiliki 1 simetri lipat
• Memiliki 1 sumbu simetri

Rumus luas segitiga yaitu :

Luas Segitiga = ½ × a × t

Rumus keliling segitiga yaitu :

Keliling Segitiga = a + b + c

Rumus mencari tinggi segitiga yaitu :

Mencari Tinggi = (2 × L) ÷ a

Rumus mencari panjang segitiga yaitu :

Mencari Panjang Alas = (2 × L) ÷ t

Keterangan :
L = Luas
a = panjang sisi alas
b = panjang sisi b
c = panjang sisi c
t = tinggi

• Segitiga Sembarang

Gambar segi banyak tidak beraturan yang kedua adalah segitiga sembarang. Segitiga sembarang adalah bangun datar segitiga yang memiliki bentuk tidak beraturan dan panjang ketiga sisinya berbeda – beda.

Segitiga sembarang yaitu memiliki panjang sisi yang berbeda beda pada ketiga sisinya. Sudut segitiga sembarang juga tidak beraturan sehingga setiap sudutnya memiliki besar sudut yang berbeda.

Sifat sifat segitiga sembarang yaitu :
• Memiliki 3 sisi yang tidak sama panjang
• Memiliki 3 sudut yang tidak sama besar
• Memiliki 1 simetri putar
• Tidak memiliki sumbu simetri
• Tidak memiliki simetri lipat

Rumus luas segitiga yaitu :

Luas Segitiga = ½ × a × t

Rumus keliling segitiga yaitu :

Keliling Segitiga = a + b + c

Rumus mencari tinggi segitiga yaitu :

Mencari Tinggi = (2 × L) ÷ a

Rumus mencari panjang segitiga yaitu :

Mencari Panjang Alas = (2 × L) ÷ t

Keterangan :
L = Luas
a = panjang sisi alas
b = panjang sisi b
c = panjang sisi c
t = tinggi

• Persegi Panjang

Segi banyak tidak beraturan yang ketiga adalah persegi panjang. Persegi panjang adalah bangun datar dua dimensi yang memiliki 4 sisi (2 pasang sisi sejajar) dan memiliki 4 sudut dengan sudut berukuran 90° atau sudut siku-siku.

Ciri ciri persegi panjang yaitu sebagai berikut :
• Memiliki 4 sisi yang terdiri dari 2 pasang sisi yang sama panjang
• 2 pasang sisi yang sama panjang posisinya saling berhadapan dan sejajar
• Memiliki 4 sudut yang sama besar berukuran 90° dan membentuk sudut siku – siku
• Memiliki 2 diagonal yang saling berpotongan
• Garis diagonal yang saling berpotongan membagi diagonal lainnya menjadi sama panjang
• Memiliki 2 sumbu simetri
• Memiliki 2 simetri lipat
• Memiliki 2 simetri putar

Rumus luas persegi panjang yaitu :

Luas Persegi Panjang = p × l

Rumus keliling persegi panjang yaitu :

Keliling Persegi Panjang = 2 × ( p + l )

Rumus mencari panjang persegi panjang yaitu :

Mencari Panjang = L ÷ l atau (K ÷ 2) – l

Rumus mencari lebar persegi panjang yaitu :

Mencari Lebar = L ÷ p atau (K ÷ 2) – p

Rumus mencari diagonal persegi panjang yaitu :

Diagonal Persegi Panjang = √ (p² + l²)

Keterangan :
L = Luas
K = Keliling
p = Panjang
l = lebar

• Trapesium

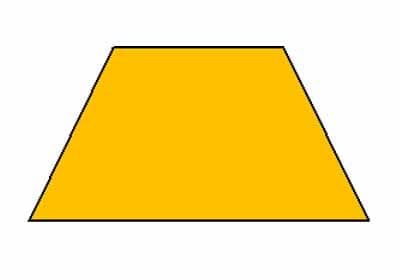
Bangun segi banyak tidak beraturan yang keempat adalah trapesium. Trapesium adalah bangun datar dua dimensi yang memiliki 2 pasang sisi yang sejajar tetapi pada 1 pasang sisinya memiliki panjang yang tidak sama atau kedua sisinya tidak sama panjang.

Ciri ciri trapesium yaitu :
• Memiliki 4 sisi dan pada 1 pasang sisinya sejajar dan saling berhadapan
• Memiliki 4 sudut, total sudutnya jika dijumlahkan berukuran 360°
• 2 sudut yang saling berdekatan jika dijumlahkan berukuran 180°
• Memiliki 2 diagonal yang sama panjang dan saling berpotongan tetapi tidak tegak lurus
• Memiliki 1 simetri putar

Rumus luas trapesium yaitu :

Luas Trapesium = ½ × (a + b) × t

Rumus keliling trapesium yaitu :

Keliling Trapesium = AB + BC + CD + DA

Rumus mencari tinggi trapesium yaitu :

Mencari Tinggi =

Rumus mencari sisi alas (AB) yaitu :

Mencari Sisi Alas (AB) =
Mencari Sisi Alas (AB) = K – CD – BC – AD

Rumus mencari sisi B (BC) yaitu :

Mencari Sisi B (BC) =
Mencari Sisi B (BC) = K – CD – AD – AB

Rumus mencari sisi CD yaitu :

CD = K – AB – BC – AD

Rumus mencari sisi AD yaitu :

Mencari Sisi AD = K – CD – BC – AB

Rumus mencari sisi BC yaitu :

Mencari Sisi BC = K – CD – AD – AB

Keterangan :
L = Luas
K = Keliling
a = Panjang Sisi Alas
b = Panjang Sisi B
AB, BC, CD, DA = panjang sisi

• Belah Ketupat

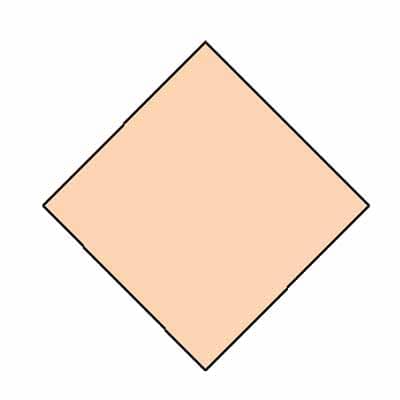
Segi banyak tidak beraturan yang kelima adalah belah ketupat. Belah ketupat adalah bangun datar dua dimensi yang memiliki 4 sisi yang sama panjang dan memiliki 2 sudut saling berhadapan yang ukurannya sama besar.

Ciri ciri belah ketupat yaitu :
• Memiliki 4 sisi dan semua sisinya memiliki panjang yang sama
• Terdiri dari 4 sudut dan sudut yang saling berhadapan sama besar
• Dua sudut yang saling berdekatan jika dijumlahkan saling berpelurus atau jika dijumlahkan besar sudutnya 180°
• Memiliki 2 diagonal yang saling berpotongan tegak lurus
• Memiliki 2 sumbu simetri atau simetri lipat
• Memiliki 2 simetri putar

Rumus luas belah ketupat yaitu :

Luas Belah Ketupat = ½ × d1 × d2

Rumus keliling belah ketupat yaitu :

Keliling Belah Ketupat = s + s + s + s
Keliling Belah Ketupat = s × 4

Rumus mencari panjang sisi belah ketupat yaitu :

Panjang Sisi = K ÷ 4

Rumus mencari panjang diagonal 1 (d1) belah ketupat yaitu :

Panjang Diagonal 1 (d1) = 2 × L ÷ d2

Rumus mencari panjang diagonal 2 (d2) belah ketupat yaitu :

Panjang Diagonal 2 (d2) = 2 × L ÷ d1

Keterangan :
L = Luas
K = Keliling
d1 = Panjang Diagonal 1
d2 = Panjang Diagonal 2
s = Panjang Sisi

• Jajar Genjang

Contoh segi banyak tidak beraturan yang keenam adalah jajar genjang. Jajar genjang adalah bangun datar dua dimensi yang memiliki 2 pasang sisi yang sejajar dan setiap pasang sisinya memiliki panjang yang sama dan memiliki 2 pasang sudut yang sama besar.

Ciri ciri jajar genjang yaitu :
• Memiliki 4 sisi yang terdiri dari 2 pasang sisi yang saling berhadapan dan sejajar
• Sisi yang saling berhadapan memiliki panjang yang sama
• Memiliki 4 sudut yaitu 1 pasang sudut tumpul dan 1 pasang sudut lancip
• Sudut yang berhadapan memiliki besar yang sama
• Dua sudut yang saling berdekatan jika dijumlahkan memiliki besar sudut 180°
• Memiliki 2 diagonal yang panjangnya tidak sama
• Tidak memiliki sumbu simetri atau simetri lipat
• Memiliki 2 simetri putar

Rumus luas jajar genjang yaitu :

Luas Jajar Genjang = a × t

Rumus keliling jajar genjang yaitu :

Keliling Jajar Genjang = 2 × (a + b)

Rumus mencari alas yaitu :

Mencari Alas = (K ÷ 2) – b atau a = L ÷ t

Rumus mencari sisi B yaitu :

Mencari Sisi B = (K ÷ 2) – a

Rumus mencari tinggi yaitu :

Mencari Tinggi = L ÷ a

Keterangan :
L = Luas
K = Keliling
a = panjang alas
b = panjang sisi b
t = tinggi

• Layang Layang

bangun datar layang layanng — gambar layang layang

Bangun segi banyak tidak beraturan yang ketujuh adalah layang layang. Layang layang adalah bangun datar dua dimensi yang memiliki 2 pasang sisi yang sama panjang dan memiliki 2 diagonal yang tegak lurus dan saling berpotongan.

Ciri ciri layang layang yaitu sebagai berikut :
• Memiliki 4 sisi yang terdiri dari 2 pasang sisi yang sama panjang
• Memiliki 4 sudut yang terdiri dari 2 pasang sudut yang saling berhadapan
• Memiliki 2 sudut yang saling berhadapan dan sama besar
• Memiliki 2 diagonal yang saling berpotongan dan tegak lurus
• 2 Diagonal yang saling berpotongan panjangnya berbeda
• Memiliki 1 sumbu simetri
• Memiliki 1 simetri lipat
• Memiliki 1 simetri putar

Rumus luas layang layang yaitu :

Luas Layang Layang = ½ × d1 × d2

Rumus keliling layang layang yaitu :

Keliling Layang Layang = a + b + c + d
Keliling Layang Layang = 2 × (a + c)

Rumus mencari panjang sisi layang layang yaitu :

Mencari Panjang A dan B = (½ × K) – c
Mencari Panjang C danD = (½ × K) – a

Rumus mencari panjang diagonal 1 (d1) yaitu :