5 Contoh Segi Banyak Beraturan : Ciri, Rumus & Gambar

Segi Banyak Beraturan – Postingan ini membahas tentang contoh segi banyak beraturan beserta contoh, macam macam dan gambarnya dengan lengkap.

Gambar segi banyak beraturan dan penjelasannya yaitu sebagai berikut.

Daftar Isi tampilkan

Segi Banyak Beraturan Adalah

Bangun segi banyak beraturan adalah suatu bangun datar dengan banyak sisi yang memiliki sisi-sisi dengan panjang yang sama dan sudut-sudut yang sama besar.

Segi banyak beraturan merujuk pada poligon dengan sisi-sisi yang memiliki panjang yang sama dan sudut-sudut yang memiliki ukuran yang sama pula. Poligon adalah bentuk geometri dua dimensi yang terdiri dari sisi-sisi lurus yang dihubungkan oleh sudut-sudut.

Dalam segi banyak beraturan, semua sisi memiliki panjang yang kongruen, artinya panjangnya sama. Selain itu, sudut-sudut dalam segi banyak beraturan juga memiliki ukuran yang sama. Kedua properti ini menciptakan simetri yang menarik pada bentuk poligon tersebut.

Contoh poligon segi banyak beraturan yang umum meliputi segi tiga sama sisi, segi empat sama sisi, dan segi lima sama sisi. Sisi-sisi pada poligon ini memiliki panjang yang sama dan sudut-sudutnya memiliki ukuran yang sama pula.

Segi banyak beraturan memiliki aplikasi dalam berbagai bidang, seperti matematika, arsitektur, seni, dan desain. Dalam matematika, segi banyak beraturan digunakan sebagai objek studi untuk mempelajari sifat-sifat geometri.

Di bidang arsitektur, segi banyak beraturan sering digunakan dalam desain bangunan untuk menciptakan kesan harmonis dan simetris. Sedangkan dalam seni dan desain, segi banyak beraturan menjadi elemen estetika yang menarik dan dapat digunakan untuk menciptakan keseimbangan visual yang menawan.

Ciri Ciri Segi Banyak Beraturan

Terdapat perbedaan antara bangun segi banyak beraturan dengan bangun segi banyak tidak beraturan. Untuk mengetahui perbedaan dari kedua jenis bangun tersebut, kita perlu mengetahui ciri ciri segi banyak beraturan.

Ciri-ciri bangun segi banyak beraturan adalah sebagai berikut :

Memiliki sisi-sisi yang memiliki panjang yang sama. Ini berarti setiap sisi pada poligon memiliki ukuran yang identik dan sejajar dengan sisi lainnya.
Memiliki sudut-sudut yang memiliki ukuran yang sama. Setiap sudut dalam poligon beraturan memiliki besaran yang seragam.
Memiliki simetri yang mencolok. Poligon ini memiliki simetri rotasi, yang berarti dapat diputar di sekitar pusatnya tanpa mengubah bentuknya. Selain itu, beberapa segi banyak beraturan juga memiliki simetri refleksi, yang berarti dapat dipantulkan pada sumbu simetri tanpa mengubah tampilannya.
Dengan sisi-sisi dan sudut-sudut yang seragam, segi banyak beraturan menciptakan keseimbangan visual yang menarik. Bentuk poligon terlihat harmonis dan simetris, memberikan kesan estetika yang memikat.
Segi banyak beraturan memiliki bentuk yang teratur dan terdefinisi dengan baik. Poligon ini memiliki tata letak yang jelas dan seragam, yang memudahkan pengamatan dan analisisnya.

Contoh Segi Banyak Beraturan

Segi banyak beraturan terdiri dari beberapa bangun datar yaitu segitiga sama sisi, persegi, segi lima beraturan, segi enam beraturan dan segi delapan beraturan.

Gambar segi banyak beraturan dan penjelasannya akan dijelaskan sebagai berikut.

• Segitiga Sama Sisi

Segi banyak beraturan yang pertama adalah segitiga sama sisi. Segitiga sama sisi adalah bangun datar segitiga yang pada ketiga sisinya memiliki panjang yang sama. Segitiga sama sisi adalah bentuk segitiga yang paling sederhana dan sering digunakan dalam matematika dan geometri.

Ciri ciri segitiga sama sisi yaitu sebagai berikut :
• Memiliki tiga sisi dengan panjang yang sama
• Memiliki tiga sudut dengan besar yang sama yaitu 60°
• Memiliki tiga simetri putar
• Memiliki tiga simetri lipat
• Memiliki tiga sumbu simetri

Rumus luas segitiga yaitu :

Luas Segitiga = ½ × a × t

Rumus keliling segitiga yaitu :

Keliling Segitiga = a + b + c

Rumus mencari tinggi segitiga yaitu :

Mencari Tinggi = (2 × L) ÷ a

Rumus mencari panjang segitiga yaitu :

Mencari Panjang Alas = (2 × L) ÷ t

Keterangan :
L = Luas
a = panjang sisi alas
b = panjang sisi b
c = panjang sisi c
t = tinggi

• Persegi

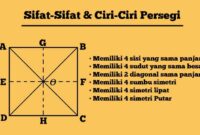
Bangun segi banyak beraturan yang kedua adalah persegi. Persegi adalah bangun datar dua dimensi yang memiliki 4 sisi (2 pasang sisi sejajar) yang keempat sisinya sama panjang dan memiliki 4 sudut yang sama besar berbentuk siku siku (90°).

Setiap sisi dan sudut pada persegi juga saling bersebrangan dan sejajar. Dalam persegi, garis yang membagi diagonal saling berpotongan pada titik tengah.

Ciri ciri persegi yaitu sebagai berikut :
• Memiliki 4 sisi dan semua sisinya memiliki panjang yang sama
• Memiliki 2 pasang sisi yang saling sejajar
• Semua sudutnya membentuk sudut siku siku atau sudut berukuran 90°
• Memiliki 2 garis diagonal yang sama panjang
• Memiliki 2 diagonal yang saling tegak lurus
• Garis diagonalnya membagi diagonal lainnya menjadi sama panjang
• 2 diagonal yang saling berpotongan membentuk sudut siku – siku
• Memiliki 4 sumbu simetri
• Memiliki 4 simetri lipat
• Memiliki 4 simetri putar
• Memiliki luas dengan rumus yaitu L = s × s
• Memiliki keliling dengan rumus yaitu K = 4 × s

Rumus luas persegi yaitu :

Luas Persegi = s × s

Rumus keliling persegi yaitu :

Keliling Persegi = 4 × s

Rumus mencari sisi persegi yaitu :

Mencari Sisi = √L atau s = K ÷ 4

Rumus mencari diagonal persegi yaitu :

Diagonal Persegi =

Keterangan :
L = Luas
K = Keliling
s = Panjang Sisi

• Segi Lima Beraturan

bangun datar segi lima — gambar segi lima

Contoh segi banyak beraturan yang ketiga adalah segi lima beraturan. Segi lima beraturan adalah bangun datar dua dimensi yang memiliki 5 sisi sama panjang dan memiliki 5 sudut yang ukurannya sama besar. Segi lima disebut juga sebagai Pentagon.

Sisi segi lima terdapat 5 sisi dengan setiap sisinya memiliki panjang yang sama. Besar sudut bangun segi lima pada setiap sudutnya adalah 108°. Jadi, total sudut pada bangun segi lima berjumlah yaitu 540°.

Ciri ciri segi lima yaitu sebagai berikut :
• Memiliki 5 sisi dan semua sisinya memiliki panjang yang sama
• Memiliki 5 sudut yang tiap sudutnya berukuran sama besar yaitu 108°
• Total sudutnya jika dijumlahkan berukuran 540°
• Memiliki 5 sumbu simetri atau simetri lipat
• Memiliki 5 simetri putar
• Memiliki 5 garis diagonal

Rumus luas segi lima yaitu :

Luas Segi Lima = ¼ √5 (5 + 2 √5) a²

Rumus keliling segi lima yaitu :

Keliling Segi Lima = 5 × s

Rumus mencari panjang diagonal segi lima yaitu :

Panjang Diagonal = ½ × (1 + √5) × s

Keterangan :
L = Luas
K = Keliling
D = Panjang Diagonal
s = Panjang Sisi

• Segi Enam Beraturan

bangun datar segi enam — gambar segi enam

Gambar segi banyak beraturan yang keempat adalah segi enam beraturan. Segi enam adalah bangun datar dua dimensi yang memiliki 6 sisi yang sama panjang dan memiliki 6 sudut yang ukurannya sama besar. Segi enam biasa disebut Hexagon.

Bangun segi enam beraturan tersusun dari 6 bangun yang berupa segitiga sama sisi yang kongruen.

Ciri ciri segi enam yaitu sebagai berikut :
• Memiliki 6 sisi dan semua sisinya memiliki panjang yang sama
• Memiliki 6 sudut dan semua sudutnya berukuran sama besar yaitu 120°
• Total sudutnya jika dijumlahkan berukuran 720°
• Memiliki 6 sumbu simetri atau simetri lipat
• Memiliki 6 simetri putar
• Memiliki 9 garis diagonal

Rumus luas segi enam yaitu :

Luas Segi Enam = 3/2 × √3 × s²

Rumus keliling segi enam yaitu :

Keliling Segi Enam = 6 × s

Rumus mencari panjang diagonal segi enam yaitu :

Mencari Panjang Diagonal = 2 × s

Rumus mencari tinggi segi enam yaitu :

Mencari Tinggi = √3 × s

Keterangan :
L = Luas
K = Keliling
D = Panjang Diagonal
t = Tinggi
s = Panjang Sisi

• Segi Delapan Beraturan

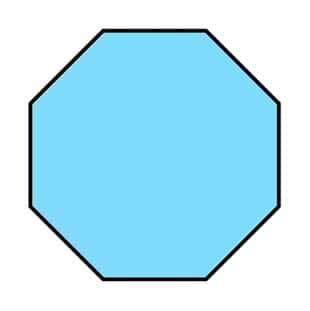
Contoh bangun segi banyak beraturan terakhir adalah segi delapan beraturan. Segi delapan adalah bangun datar dua dimensi yang memiliki 8 sisi yang sama panjang dan memiliki 8 sudut yang sama besar.

Segi delapan sering digunakan sebagai dasar untuk membuat simbol stop dalam lalu lintas.

Ciri ciri segi delapan yaitu sebagai berikut :
• Memiliki 8 sisi dan semua sisinya memiliki panjang yang sama
• Memiliki 8 sudut dan semua sudutnya berukuran sama besar yaitu 135°
• Jumlah sudut pada bangun segi delapan adalah 1080°
• Memiliki 8 sumbu simetri atau simetri lipat
• Tidak memiliki simetri putar

Gambar segi banyak beraturan beserta penjelasannya sudah diberikan dengan lengkap diatas. Semoga tulisan ini bisa bermanfaat bagi para pembaca. Jika terdapat kekurangan atau kesalahan dalam penulisan dan ingin memberikan kritik atau saran, bisa ditulis di kolom komentar.